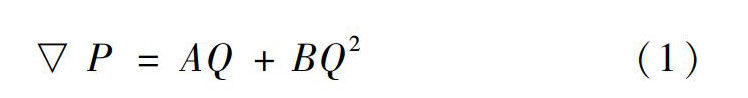
打开文本图片集
摘要:针对裂隙岩体非达西渗流问题,开展了不同粗糙裂隙非线性渗流特性的研究。将完整的方形岩块采用劈裂法制成裂隙试件,用三维光学扫描系统量测裂隙表面形貌,并采用Kulatilake提出的自仿射分形维度方法计算表面的分形维度来表征粗糙表面的各向异性特征。根据裂隙流的曲折效应,在Forchheimer定律基础上,提出了水文弯曲度和表面分形幂律关系来表征非线性特点,并由此提出了新的粗糙裂隙非线性分形模型。对各组裂隙试件在2个方向(0°,90°)上进行饱和渗流试验,发现流动符合Forchheimer定律且存在各向异性特点,最后由分形模型,提出了区分达西流与Forchheimer流的新判据。
关键词:岩石裂隙; 非线性渗流; 分形维度; Forchheimer定律; 各向异性; 临界雷诺数
中图法分类号:P641.2文献标志码: ADOI:10.16232/j.cnki.1001-4179.2019.02.031
1研究背景
漫长的地质作用和人类活动造成岩体被大量的断层、裂隙切割,这些结构面及其构成的网络成为地下水流动的主要通道,并由此控制着岩体的渗透特性。在岩体水力学研究中,通常将结构面概化为2块光滑的平行板,通过理论和试验得到著名的立方定律。由于实际结构面粗糙起伏、零星接触或含有充填物等,许多学者据此提出各种修正模型。
在某些工程中,如河谷深厚覆盖层建坝、低渗透油气井开采、煤矿瓦斯突出等[1]都会出现高水力梯度现象,这时流体流动的机制和规律将发生重大改变,用立方定律或其修正模型会造成较大的偏差。一般引用多孔介质的非线性渗流模型Forchheimer定律[2]来描述这种渗流行为
▽P=AQ+BQ 2(1)
式中,▽P为单位渗流长度的压力差,Q为通过裂隙的流量,A和B分别为黏性系数和惯性系数。
Zimmerman等[3]通过试验和数值的方法,观察到雷诺数Re>20时,粗糙裂隙的Forchheimer流现象;Zhang等[4]探讨了不同围压下,粗糙裂隙线性和非线性流动特性;Zhou等[5]利用不同围压的压水试验,解释了Forchheimer流系数A和B的物理意义,及内部过渡机制,但对裂隙面粗糙性对非线性流动的影响没有详细阐明。Chen等评价了Forchheimer判据方程的系数[6]。金毅等[7]从细观层面上指出粗糙几何对裂隙流的影响表现在三个方面:① 流体内部的摩擦效应;② 裂隙面的曲折效应;③ 局部粗糙度效应。Tsang等[8]认为裂隙面的粗糙性会引发流动的曲折性;肖维民等[9]引入曲折因子描述这种流动的曲折现象。
自分形几何被B.B.Mandelbrot提出以后,谢和平等[10]首先将其引入到裂隙粗糙度的描述,后来又用来描述岩体断裂面渗流特征[11];Murata等[12]研究了分形参数对曲折效应的影响;王刚等[13]提出了考虑分形特征的节理面渗流公式;Ju等[14]对不同分形维度粗糙单裂隙物理模型进行水渗流试验,阐明了粗糙结构对渗流的影响;Develi等[15]对7种人工张拉型裂隙面进行饱和渗流试验,并用分形维度描述粗糙度,研究了粗糙度、各向异性和法向应力对渗流特征的影响。
本文从曲折效应对裂隙流非线性作用强度和方式入手,并结合裂隙自仿射分形特点,推导了粗糙裂隙非线性分形模型。并结合渗流试验,分析了Forchheimer流的规律和各向异性,并验证了新模型。
2粗糙裂隙非线性分形模型
Forchheimer流动定律包含两个部分:线性部分AQ和非线性部分BQ 2,体现出达西渗流和非达西渗流。在低流速阶段,一般可用立方定律描述流量和压力的线性关系,则黏性系数A可表示为
A=12μwe 3h(2)
式中,μ为流体的黏性系数,w为裂隙的宽度,eh為水力开度,是在初始阶段根据立方定律反求而得,eh=(12μQ/w/▽P)1/3。
惯性系数B体现了渗流曲线偏离线性段的程度。Schrauf等[2]通过量纲分析,提出
B=bDρe 3hw 2(3)
式中,ρ为流体密度,bD是与裂隙面结构特征有关的参数。Chen等[6]用绝对粗糙度描述裂隙面几何特征,提出的双参数模型为
bD=a(ξ2eh) b(4)
式中,a和b为拟合参数。但仅仅用绝对粗糙度ξ表征裂隙面粗糙程度的影响,不能反映流动的曲折性和各向异性。郭建春等[16]通过数值方法研究了裂隙流的非达西效应,结果表明表面越粗糙,隙宽分布越复杂,流动时流态将越不稳定,曲折效应将增加,在高流速下会出现涡流和回流现象,增大惯性阻力。为了表征曲折性的影响,提出如下幂律关系
bD=cτ aτ bs(5)
式中,a,b和c为拟合参数;τ为水文弯曲度,定义为流体实际渗流路径长度Lt与沿裂隙水头压力梯度方向的水平长度Lc之比。τs为裂隙面曲折率,定义为裂隙面表面积As与投影面积Ac之比。对于具有分形特征的裂隙,测度F(δ)与测量尺度δ存在如下关系
F(δ)=F0δ(6)
式中,与分形维数D有关,即=f(D),D∈(1,3);F0为直观测度。边长为δ1的正方形网格覆盖的裂隙表面总的面积AS与δ1存在如下关系
AS=F1δ2-DS1(7)
式中,DS为裂隙面面积分形维度,对于正方形裂隙,当δ1=Lc时,将(7)式代入AS(Lc)=Ac得:
F1=ADS2c(8)
由τs的定义,有
τs=AS(δ1)Ac=(δ 21Ac)2-DS(9)
同理,对于渗流路径长度Lt同观测尺度δ2存在如下分形关系:
