打开文本图片集
摘要:为改善水轮发电机电能质量,预防阻尼绕组过热,保证机组与电网运行安全,基于电机电磁场、电路及传热学理论,建立了水轮发电机三维分层非线性时变运动电磁场一电路结合模型与磁极系统三维稳态温度场模型。进而针对一台q=1(1/2)的36 MW贯流式机组的128种结构设计方案,通过电磁场一温度场综合计算,广泛深入地分析了定转子槽距比、定子斜槽程度以及每极阻尼条根数等结构参数对空载电压波形畸变率和额定工况阻尼绕组损耗发热的影响,在此基础上,讨论了同时抑制空载电压波形畸变率与阻尼绕组损耗发热的设计措施。计算结果与实测数据相吻合。关键词:贯流式水轮发电机;空载电压波形畸变;阻尼绕组损耗与发热;电磁场;温度场
DOI:10.15938/j.emc.2016.04.003
中图分类号:TM 312 文献标志码:A 文章编号:1007-449X(2016)04-0017-10
0 引言
由电压谐波引发的空载电压波形畸变,可能对水轮发电机电能质量与并网运行安全造成不利影响。作为水轮发电机的重要组成部分,阻尼绕组是发电机与电网安全稳定运行的重要保障。在发电机设计阶段,定转子槽距比、每极阻尼条根数、以及定子斜槽等结构参数的选取,不但影响着阻尼绕组损耗发热分布,还对空载电压波形有着密切影响。特别是对于近年在低水头大流量电站广泛应用的贯流式水轮发电机而言,在其设计制造与运行中,不但面临电压谐波导致空载电压波形畸变的难题,还屡次在额定负载工况下发生阻尼条过热故障。为改善贯流式水轮发电机电能质量,预防阻尼绕组过热断条故障,保证运行安全,很有必要采用电磁场与温度场综合分析方法,针对其空载电压波形畸变率与阻尼绕组损耗发热抑制问题,进行全面深入的研究。
在水轮发电机空载电压波形分析与优化方面,早期文献多采用电磁场解析法或电路磁路法进行研究。其中,文献着重研究了发电机附加磁场与谐波电动势的解析计算;文献则在上述文献成果的基础上,较为全面地分析了增大气隙、采用分数槽绕组、采用定子斜槽或转子斜极、改善极靴表面形状、移动磁极位置、改变阻尼绕组几何形状等方法对空载电压波形的改善效果。以上解析方法具有概念清晰,便于工程人员理解的优点,然而由于难以考虑铁磁材料饱和、定子斜槽、转子旋转及阻尼条涡流等因素的影响,其定量计算的精确度尚有较大提升空间。为克服上述缺陷,近年来,国内外研究者多使用数值计算方法,开展水轮发电机空载电压波形分析研究,取得了较大进展。文献通过建立凸极同步发电机的运动电磁场时步有限元计算模型,研究了空载电压波形。文献将解析法与有限元方法相结合,计算分析了叠片式凸极同步发电机的空载电压波形,并初步讨论了阻尼绕组偏心0.25倍定子节距对空载电压波形质量的影响。文献将多回路法与电磁场有限元法相结合,用于求解凸极同步发电机电压波形。文献通过建立水轮发电机二维场路耦合时步有限元计算模型,分析了不对称磁极设计方案对空载电压波形的优化效果。
针对阻尼绕组电流、损耗与发热计算问题,文献将阻尼绕组电路网络分析与解析法建模相结合,研究了阻尼条电流波形。文献通过建立凸极电机谐态电磁场有限元计算模型,分别求解了暂态和稳态阻尼条电流。文献将水轮发电机静态电磁场与谐态电磁场有限元模型结合使用,求解了阻尼条损耗。文献应用运动电磁场时步有限元模型,计算了水轮发电机额定与负序工况下的阻尼条电流与损耗。文献使用三维等参元模型,计算了水轮发电机转子稳态温度场。文献基于流场一温度场模型,研究了转子的气体流动和发热情况。
文献综合运用二维运动电磁场有限元模型与三维温度场模型,初步探讨了不同结构与材料参数对阻尼绕组损耗发热的影响。在此基础上,文献通过建立分层运动电磁场模型与三维温度场模型,针对5种定转子槽距比方案与1种定子斜槽方案,开展了空载波形与阻尼绕组损耗发热计算分析。但上述两篇文献所讨论的设计方案较为有限,其研究广度和深度尚待进一步提高。
鉴于此,本文在文献的基础上,以抑制空载电压波形畸变率与阻尼条发热为目标,通过建立三维多层运动电磁场与电路相结合的时步有限元模型与三维温度场有限元模型,以1台36 MW分数槽大型贯流式水轮发电机(q=1(1/2))为算例,针对常规设计手册上q=1(1/2)分数槽机组常用的每极阻尼条根数nb=4与nb=3以及定转子槽距比与定子斜槽程度取值范围,选定4类共128种不同的定转子槽距比、定子斜槽程度设计方案,分析计算了该机组空载电压波形畸变率与额定负载工况阻尼条损耗发热分布随上述结构参数变化的规律,在此基础上,探讨了同时抑制上述两项参数的结构设计措施。
1 电磁场计算模型
1.1 发电机基本参数
作为算例的贯流式水轮发电机型号为SFWG36-72/7350,其基本参数见表1。
选定以下4类共128种结构设计方案进行研究,其编号及含义见表2,nb为每极阻尼条根数,其中t1为定子齿距,并保持不变,t2为转子阻尼绕组节距,可调节,t2/t1为定转子槽距比,△t2/t1为槽距比变化步长。△skew为定子斜槽程度变化步长。
1.2 运动电磁场边值问题
根据磁场分布的周期性,选定1对磁极的范围作为发电机电磁场的求解区域,并沿轴向将该发电机分为12段,以便准确分析斜槽方案,参见图1。
在求解区域内,考虑到铁心的饱和效应,描述非线性时变运动电磁场问题的偏微分方程为(1)式中:4为矢量磁位;Js为外部强加的源电流密度;v为媒质的磁阻率;V为媒质相对于参考坐标系的运动速度;σ为媒质的电导率。
在三维多层运动电磁场模型中,对每一层而言,设电流密度和矢量磁位只有z轴分量,速度只有x轴分量。引入库仑规范▽·A=0,加入边界条件,便可得到发电机二维非线性时变运动电磁场的边值问题:(2)式中:Vx为速度的x轴分量;Jslz为源电流密度的z轴分量;Aslz为矢量磁位的z轴分量,它在转子磁轭内侧圆弧arc_in和定子磁轭外侧圆弧arc_out上满足第1类齐次边界条件,在电角度0度及360度的磁极分界线cyclic_boundary_start和cyclic_boundary_end上满足整周期性边界条件。
1.3 定转子电路模型
为了考虑定子绕组端部和转子阻尼绕组端环的影响,并能灵活设置运行工况,建立了相应的定转子电路模型,把外电路方程和电磁场方程结合起来进行求解。
根据如图2所示的定子绕组负载电路,可得到定子回路的电压方程式(3)式中:es为定子相绕组直线部分感应电动势,通过有限元计算得到;us和is分别为定子绕组端电压和相电流;R1e和L1e分别为定子相绕组端部的电阻和漏电感。
而图中的RL和LL为发电机的负载电阻与负载电感,通过改变它们的设置值,能够设定发电机运行的不同工况。
根据图3所示的阻尼绕组电路结构,设iM、iM+1分别为第M根阻尼条左、右两侧的端环电流,它们与第M根阻尼条的电流iBM之间满足下列关系(4)
第M根和第M+1根阻尼条之间满足下列电压方程(5)式中R2e和L2e分别阻尼绕组端环的电阻和电感。
设求解区域内有N根阻尼条,根据周期条件,可确定边界处电流和电压的约束条件为:(6)(7)
将发电机定转子电路方程与电磁场边值问题方程联立,并设置负载电阻与电感,进行时间与空间离散,即可通过时步有限元计算,求出各层的矢量磁位Aslz,进而得出相应工况下的磁密、电压、电流以及损耗等计算结果。
1.4 发电机空载电压的计算
在图2中,设负载电阻RL及电感LL为无穷大,即可分析计算发电机的空载运行状态。通过时步有限元计算,即可求出空载线电压(8)式中:Ncl为模型分层数,Ns为定子每相绕组串联导体数;LsL为两层之间定子铁心有效长度;S为每层中一相绕组电流分布区域;Ⅳ为该相绕组区域的剖分单元数;S+i和S-i分别为每层中该相绕组电流流入和流出一个单元的区域;Aslzi为该单元的矢量磁位平均值。
根据国家标准GB/T 1029-2005规定,实际线电压波形与正弦波形的偏差程度一般用电压波形正弦性畸变率来表示,其值由下式确定(9)式中:U为线电压的有效值;Un为线电压中n次谐波的有效值。
对于大型发电机,国家标准规定,必须满足HDF≤5%。
1.5 额定负载时阻尼绕组损耗的计算
在图2中,设负载电阻RL及电感LL为额定值,即可分析计算发电机的额定负载运行状态。
对于分层模型的第j层而言,第k根阻尼条的涡流密度为:(10)式中:σb为阻尼条电导率;Lb为阻尼条长度;uk为第k根阻尼条电压。
由此可得该阻尼条在第j层的1个剖分单元对应的电流和损耗分别为:(11)(12)式中:Lbsl为阻尼条位于模型第j层的长度;△e为该层阻尼条区域内1个剖分单元的面积
因此,整根阻尼条的涡流损耗可由下式计算(13)式中:k为单层内1根阻尼条区域的剖分单元总数;Ncl为模型分层数。
2 转子三维温度场模型
2.1 求解区域及其剖分
设发电机通风系统结构对称,转子温度分布关于其中心断面对称。这时,可把温度场的求解区域定为1个磁极从转子端面到中心断面的半个轴向段,该区域由转子铁心、阻尼绕组、励磁绕组、托板等部件组成.如图4所示。
2.2 转子三维温度场边值问题
考虑到转子磁极导热能力的各向异性特点,求解区域内的三维稳态温度场边值问题为:(14)式中:T为待求温度,℃;Ax、Ay、Az分别为x、y、z方向上的导热系数,W/(m·℃);g,为热源密度,W/m3;S2为满足绝热边界条件的转子中心断面及转子与磁轭交界面;S3为满足散热边界条件的各边界面;α为S3边界面上的散热系数,W/(m2·℃);Tf为S3边界面上的温度。
2.3 散热系数的确定
转子旋转时,极靴上表面的散热系数和励磁绕组的散热系数分别为:(15)(16)式中:丁为极距,cm;K、α"根据电机结构确定。而考虑到转子迎风面的散热能力优于背风面,在确定其散热系数时,应分别乘以1个比例系数。此处迎风面和背风面的比例系数分别取1.2和0.8,端面的散热系数取迎风面和背风面的平均值。
3 计算结果与分析
3.1 空载电压波形与谐波分析
针对所列的4类128种设计方案,进行时步有限元计算与空载电压分析。由于空载线电压Uab、Ubc、Uca对称,因此仅讨论Uab。部分计算结果如图5至图12所示。
由图5与图6可见,无论每极阻尼条根数nb=4还是nb=3,以下趋势都存在:
1)当定子未斜槽时,对于t2/t1而言,当其取值位于0.5~0.6与0.85~0.93区间时,HDF较大,波形质量较差,而当其取值位于0.75~0.85区间时,HDF较小,波形质量较好。
2)定子斜槽对HDF的抑制作用非较为明显,即使t2/t1取0.93这样HDF很大的方案,采取适当的斜槽措施后,其HDF仍然可以抑制到1%以下,从而获得较好的空载电压波形质量。
3)不同定子斜槽程度,对HDF的抑制效果不同,其中斜0.25槽、0.55槽与0.8槽方案对HDF抑制效果相对较差,而斜0.4槽、0.45槽、0.5槽、0.6槽、0.9槽与1槽方案对HDF的抑制效果较好,其中斜0.45槽与斜1槽的方案最好。
4)对比图5中不同阻尼条根数nb所对应的HDF曲线可知,当仅采用调节t2/t1的方式优化空载电压波形时,较大nb的可能会更有效地抑制HDF,因此可能获得更好的空载电压波形。而由图6中不同阻尼条根数nb所对应的HDF曲线可见,对于nb=4与nb=3两种情况,其HDF随着斜槽程度增大而变化的曲线形状相似,但较大的nb仍然有助于抑制HDF。
为进一步探讨造成上述结果的原因,对空载电压进行谐波分析。在进行谐波分析时,应注意考虑齿谐波的影响。这类谐波在频谱中次数为
v=k2mq±1。 (17)式中:k为齿谐波阶数;m为相数;q为每极每相槽数。对该电机而言,由于m=3,q=1(1/2),因此1阶和2阶齿谐波次数分别为8次与10次,17次与19次。
除此之外,还应注意分析其余高次谐波分量的影响。
对部分方案进行谐波分析后,所得空载电压谐波分布情况如图7与图8所示。
由图7与图8可见,对空载电压波形影响较大的谐波,除了属于2阶齿谐波的17次和19次谐波之外,还有27次和29次谐波。
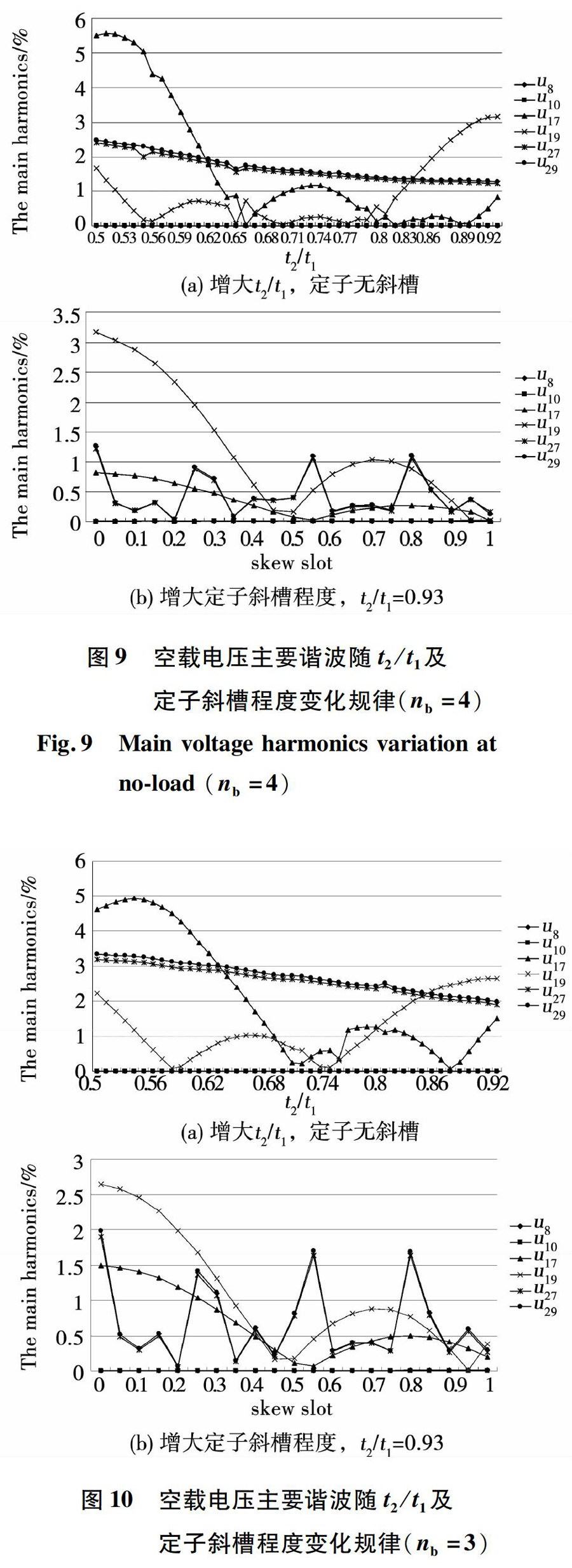
随后对所有设计方案的一阶与二阶齿谐波及27次和29次谐波的分布及变化情况进行分析,得出一阶与二阶齿谐波及27次和29次谐波随t2/t1及定子斜槽程度变化的趋势如图9与图10所示。
由图9与图10可见,无论每极阻尼条根数nb=4还是nb=3,在本次研究的t2/t1与定子斜槽程度变化区间内,一阶齿谐波(8次与10次)的影响都可以忽略,而二阶齿谐波(17次与10次)及27次和29次谐波较为明显。
因此,为进一步分析二阶齿谐波和27次与29次谐波对HDF的影响,设参数Fu如式(18)所示。(18)
随后得出Fu随t2/t1及定子斜槽程度变化的情况,如图11与图12所示。
由图9与图12可知:
1)无论是Fu随着t2/t1变化的曲线,还是Fu随着定子斜槽程度变化的曲线,其形状变化规律都与图5与图6所示的HDF随上述2个结构参数变化的曲线基本相同,由此进一步表明,对于此次研究的每极每相槽数为1(1/2)贯流式水轮发电机,影响其空载电压HDF的主要谐波为二阶齿谐波17次与19次,以及27次与29次谐波。
2)当定子不斜槽时,随着t2/t1的增大,27次与29次谐波持续减小,但在t2/t1的某些取值区域,二阶齿谐波(17次与19次)仍然较为明显,因此HDF较大,空载电压波形质量较差,如t2/t1取值位于0.5~0.6与0.85~0.93区间的情况。只有当t2/t1取值位于上述两类谐波都较小的区域时,HDF较小,空载电压波形质量较好,如t2/t1取值位于0.75~0.85区间的情况。
3)采用调整定子斜槽的措施抑制HDF时,对二阶齿谐波(17次与19次)的削弱较为明显,但某些斜槽方案仍然存在较为明显的27次与29次谐波,因此其HDF较大,空载电压波形质量较差,如斜0.25槽、斜0.55槽及斜0.8槽的情况。只有上述两类谐波都较小的方案,才会有较小的HDF与较好的空载电压波形质量,如斜0.4槽、0.45槽、0.5槽、0.6槽、0.9槽与1槽方案。
4)对比上述HDF较小的斜槽方案可以发现,其HDF较为接近,特别是效果最好的斜0.45槽方案与斜1槽方案,其HDF几乎相同。如表3所示。这就意味着采用较小的斜槽程度,如斜0.45槽或斜0.5槽,可以获得接近于斜1槽的优质波形。
3.2 阻尼条损耗发热分析
发电机额定负载工况下,阻尼条损耗发热计算结果如图13到图16所示,其中,∑P为一个磁极上的阻尼绕组总损耗,Tmax表示阻尼绕组最高温度。
由此可知,无论每极阻尼条根数nb=4还是nb=3,以下趋势都存在:
1)采用调整t2/t1的措施,对阻尼条损耗发热的影响较为明显,其中,当t2/t1的取值位于0.85~0.93区间时,阻尼条损耗发热较小。
2)采用定子斜槽措施,对阻尼条损耗发热具有一定的抑制作用,但效果远不如调整t2/t1。
3)如果仅采用调整t2/t1的措施来抑制阻尼条损耗发热,当t2/t1取值位于某些区间时,阻条损耗发热较小,但空载电压HDF较大,空载电压波形质量较差,如t2/t1的取值位于0.85~0.93的情况;而当t2/t1取值位于另一些区间时,空载电压HDF较小,空载电压波形质量较好,但阻尼绕组损耗发热相对较大,如t2/t1取值位于0.75~0.85与区间的情况。
4)针对t2/t1的取值位于0.85~0.93区间的设计方案,采取斜槽措施,既可以获得较低的HDF与较好的空载电压波形,又可以获得较低阻尼绕组损耗发热。即使是波形质量较差的t2/t1=0.93的方案,在采用斜0.4槽、0.45槽、0.5槽、0.6槽、0.9槽与1槽等方案后,也能获得较好的空载电压波形与较低的阻尼绕组发热。且对比上述几种斜槽方案可知,其阻尼条最高温度Tmax十分接近,这就意味着,采用较小的斜槽程度,如斜0.45槽或斜0.5槽,可以获得接近于斜1槽的较低的损耗和发热,如表4所示。
5)对比不同的阻尼条根数nb所对应的Tmax可知,无论是采用调整t2/t1的措施,还是采用斜槽措施,当阻尼条根数nb较少时,阻尼条的损耗发热相对较低。
3.3 空载波形计算结果验证
为了验证计算的准确性,针对算例机组真机实际采用的方案(nb=4,t2/t1=0.93,定子斜0.5槽),进行了空载电压测量。
试验所需仪表如表5所示。
测量中时间采样频率设置为0.01 ms,并对空载电压波形进行傅里叶分析,谐波频率分析到5 000Hz。对发电机空载相电压和线电压分别进行了测量。测量接线图与结果界面见图17与图18。
空载线电压波形测量结果数据如表6所示。
由对比可见,对空载电压波形的计算分析结果与测量值较为吻合,准确性较高。
4 结论
对于本文研究的每极每相槽数为1(1/2)的贯流式水轮发电机而言,其空载电压HDF不但受到二阶齿谐波的影响,还受到27次与29次等高次谐波的影响。只有同时抑制上述两类谐波,才有可能获得较低的HDF和较好的空载电压波形质量。
无论是单纯增大阻尼绕组节距t2,还是单纯调节定子斜槽程度,或是单纯改变每极阻尼条根数,都难以全面保证对空载电压波形畸变率和阻尼绕组损耗发热的抑制效果。
只有在合理增大nb与t2的同时,采用合理的斜槽措施,如斜0.4槽、0.45槽、0.5槽、0.6槽、0.9槽与1槽等方案,才有可能同时获得较好的空载电压波形和较低的条损耗发热。如本文机组实际采用的nb=4,t2/t1=0.93,定子斜0.5槽方案,就是一种较为满意的方案。
本文的计算模型,能够较为精确地预测各种结构设计方案对水轮发电机空载电压波形与阻尼绕组发热的影响,从而能够为水轮发电机设计制造、发电机与电网的运行保护,提供更为有益的参考。
(编辑:贾志超)